Methodologies of Group Sequential and Adaptive Designs

Gernot Wassmer

September 29, 2025

Overview

• Introduction

• Some Theory First

• Group Sequential Designs

• Confirmatory Adaptive Designs

• Adaptive Designs with Treatment Arm Selection

• Discussion

Introduction

rpact 📦

• Comprehensive validated R package implementing methodology described in Wassmer and Brannath (2016)

• Enables the design of traditional and confirmatory adaptive group sequential designs

• Provides interim data analysis and simulation including early efficacy stopping and futility analyses

• Enables sample-size reassessment with different strategies

• Enables treatment arm selection in multi-stage multi-arm (MAMS) designs

• Enables subset selection in population enrichment designs

• Provides a comprehensive and reliable sample size calculator

Developed by RPACT 🏢

• RPACT company founded in 2017 by Gernot Wassmer and Friedrich Pahlke

• Idea: open source development with help of “crowd funding”

• Currently supported by 21 companies

• \(>\) 80 presentations and training courses since 2018, e.g., FDA in March 2022

• 29 vignettes based on Quarto and published on rpact.org/vignettes

• 28 releases on CRAN since 2018

Some Theory First

The classical (frequentist) paradigm for testing a hypothesis

• Fix significance level

• Fix endpoint and hypothesis

• Fix type of test and test statistic

• Fix (compute) sample size under specified effect size, variability, and power

• Observe patients, compute p-value for specified hypothesis

• Make test decision.

A Practical Example

• A clinical trial for the comparison of a new blood pressure lowering drug A as compared to standard medication B is planned. It is assumed that blood pressure lowering is normally distributed with standard deviation \(\sigma = 15\).

• The researcher team assumes that A lowers the blood pressure on average by 20mmHg, whereas B lowers only on average by 10mmHg.

• Propose a sample size for this study at level \(\alpha = 0.025\) and power 80%.

• The statisticians penetratingly asks if the standard deviation can be \(\sigma = 20\), and even the difference in blood pressure lowering might be only 5mmHg (which is clinically relevant, too). So the team might be overoptimistic.

What can be proposed?

Single Fixed Sample

• \(\alpha = 0.025\) (one-sided), \(1-\beta = 0.80\)
• Relevant (expected) effect \(\delta^* = 10\)
• Standard deviation \(\sigma = 15\)
• Sample size per treatment group \(n = 37\).

Caution

No early stopping of the trial Win or loose

Caution

No possibility to adjust in case of
- Over or underestimation of effect size
- Over or underestimation of variability

Internal Pilot Studies

• Wittes and Brittain (1990), Gould (1992)
• Blinded sample size reassessment
• Use overall variance at interim to adjust sample size
• No early efficacy or futility stop
• Virtually negligible effect on Type I error rate (Kieser and Friede (2000), Friede and Kieser (2001), Friede and Kieser (2006), …)

Group Sequential Design

• \(\alpha = 0.025\) (one-sided), \(1-\beta = 0.80\), \(\delta^* = 10\), \(\sigma = 15\)
• Four-stage group sequential design with constant critical boundaries
• Maximum sample size per treatment group \(4 \cdot 11 = 44\)
• Average (expected) total sample size under \(\delta^* = 10: 58.5\)

Possible

Interim looks to assess stopping the trial early either for success, futility or harm

Caution

No possibility to adjust in case of
- Over or underestimation of effect size
- Over or underestimation of variability

\(\hspace{1cm}\)

Caveat

Don’t fix the subsequent sample sizes in a “data driven” way. This could lead to a serious inflation of the Type I error rate. The effects of not considering this is described, e.g., in Proschan, Follmann, and Waclawiw (1992).

Furthermore, you have to fix the designing parameters (e.g., shape of decision boundaries, the test statistic to be used, the hypothesis to be tested) prior to the experiment. These cannot be changed during the course of the trial.

Adaptive Confirmatory Designs

Possible

Interim looks to assess stopping the trial early either for success, futility or harm

\(\hspace{1cm}\)

Possible

Possibility to adjust in case of
- Over- or underestimation of effect size
- Over- or underestimation of variability

\(\hspace{1cm}\)

… and even much more

Group Sequential Designs

Group Sequential Designs: Basic Theory

Pocock and O’Brien and Fleming design
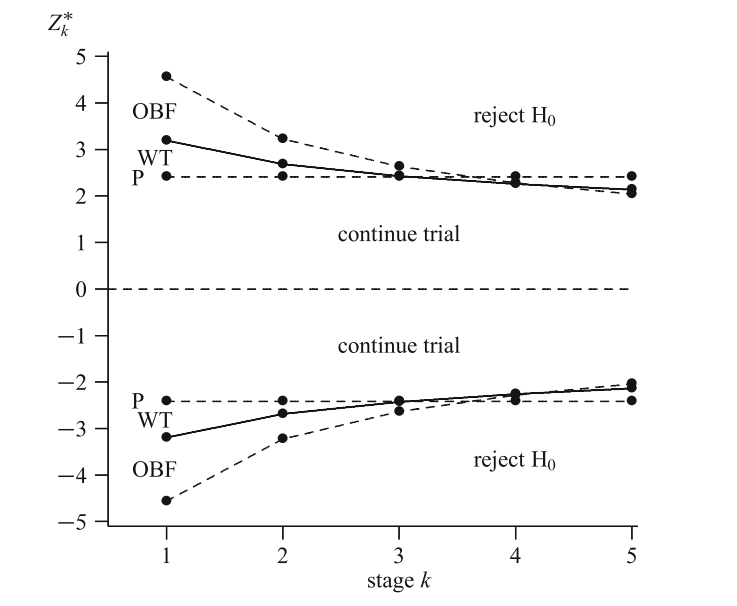
Wang and Tsiatis \(\Delta\)-class \(u_k = k^{\Delta-0.5}\). O’Brien and Fleming: \(\Delta\) = 0; Pocock: \(\Delta\) = 0.5

How this is done with rpact

library(rpact)
getDesignGroupSequential(kMax = 5,
            typeOfDesign = "WT", deltaWT = 0.25)  |>
    plot()

getDesignGroupSequential(kMax = 5,
            typeOfDesign = "WT", deltaWT = 0.25)  |>
    summary()

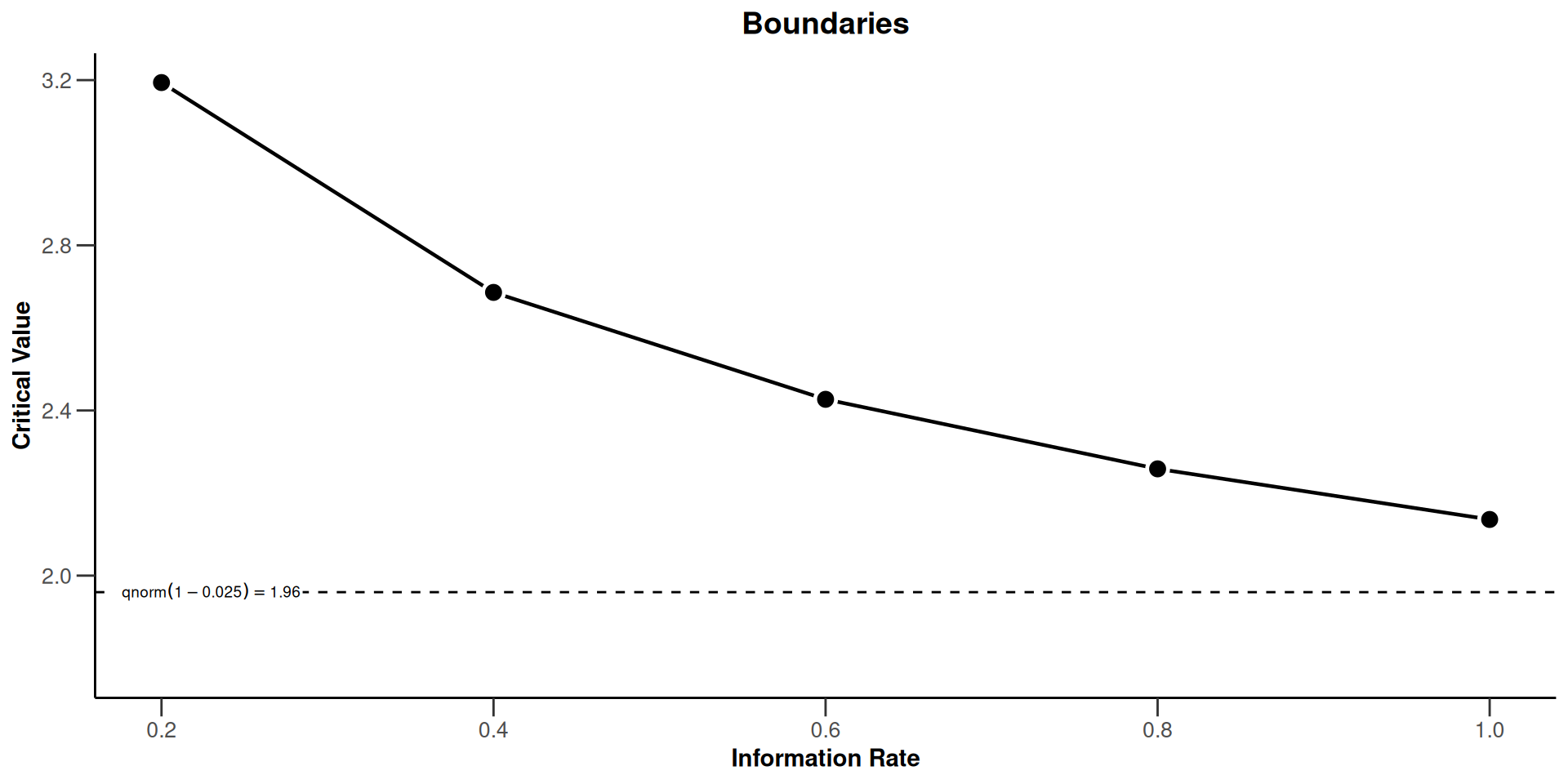
Sequential analysis with a maximum of 5 looks (group sequential design)

Wang & Tsiatis Delta class design (deltaWT = 0.25), one-sided overall significance level 2.5%, power 80%, undefined endpoint, inflation factor 1.0718, ASN H1 0.7868, ASN H01 0.9982, ASN H0 1.0651.

Stage	1	2	3	4	5
Planned information rate	20%	40%	60%	80%	100%
Cumulative alpha spent	0.0007	0.0041	0.0098	0.0170	0.0250
Stage levels (one-sided)	0.0007	0.0036	0.0076	0.0120	0.0163
Efficacy boundary (z-value scale)	3.194	2.686	2.427	2.259	2.136
Cumulative power	0.0289	0.2017	0.4447	0.6544	0.8000

Group Sequential Designs: Basic Theory

Many other designs

• Wang and Tsiatis class

• Haybittle and Peto \(u_1 = \ldots = u_{K-1} = 3\), \(u_K\) accordingly

• One-sided tests

• Futility stopping

Also:

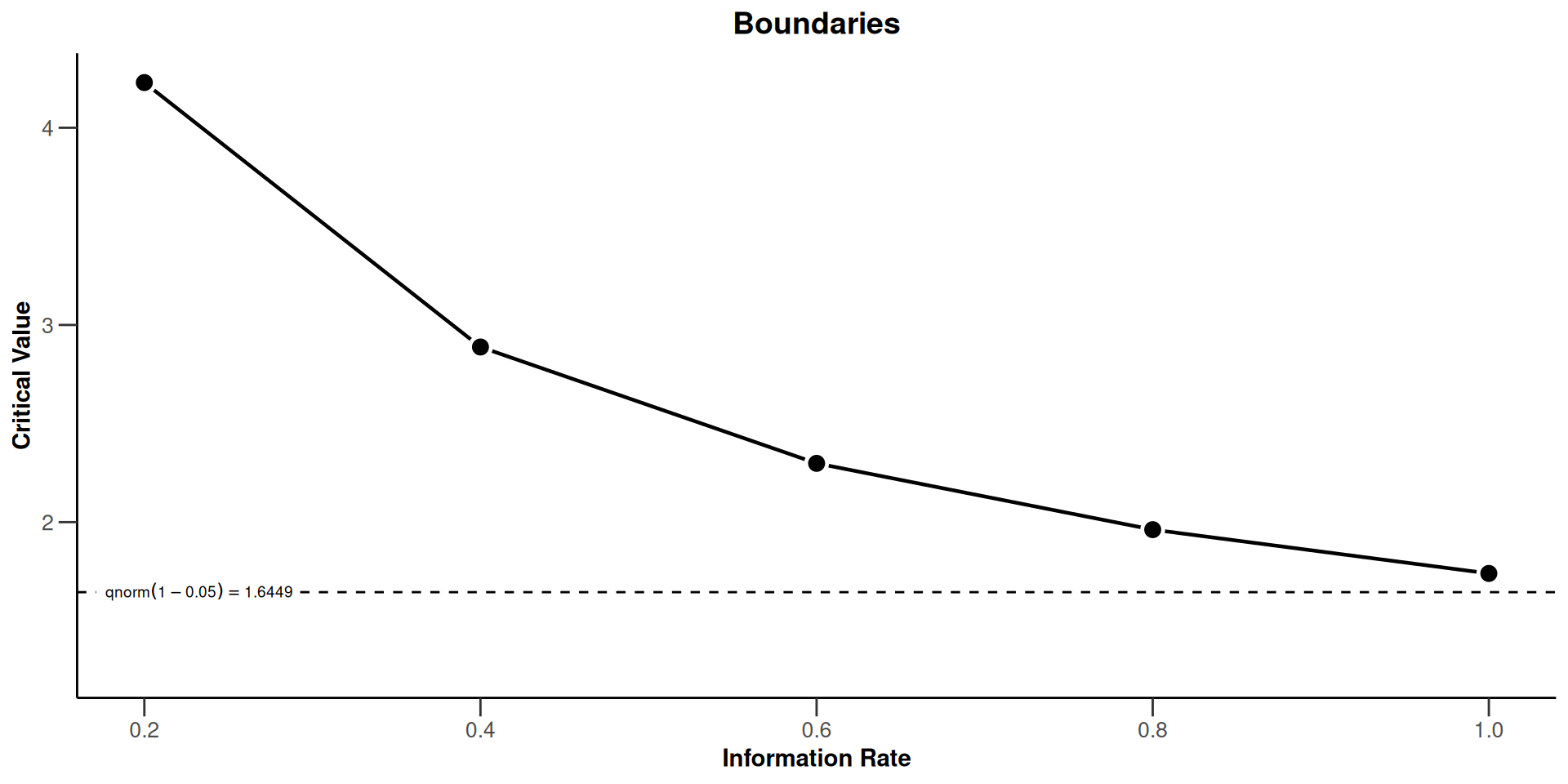
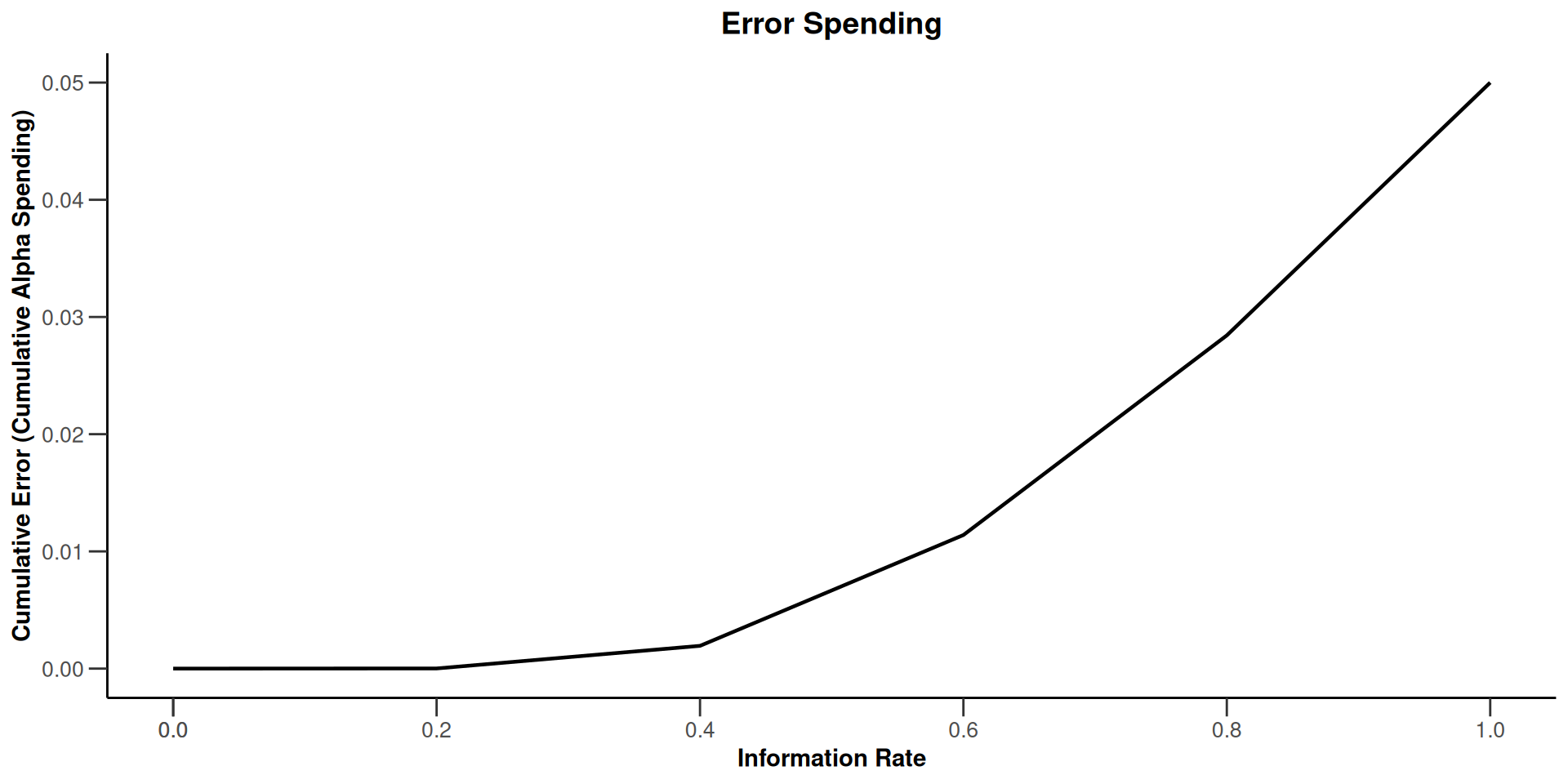
• \(\alpha\)-spending or use-function approach: Specification of the critical values through the use of a function that determines how the significance level is spent over the interim stages.

The Use Function Approach

Examples of \(\alpha\)-spending functions

Examples of \(\alpha\)-spending functions. \(\alpha_1^*\) and \(\alpha_2^*\) approximate O’Brien and Fleming’s and Pocock’s design, respectively. \(\alpha_3^*(\varrho)\) is plotted for \(\varrho = 1.0\), \(1.5\), and \(2.0\); \(\alpha = 0.05\).

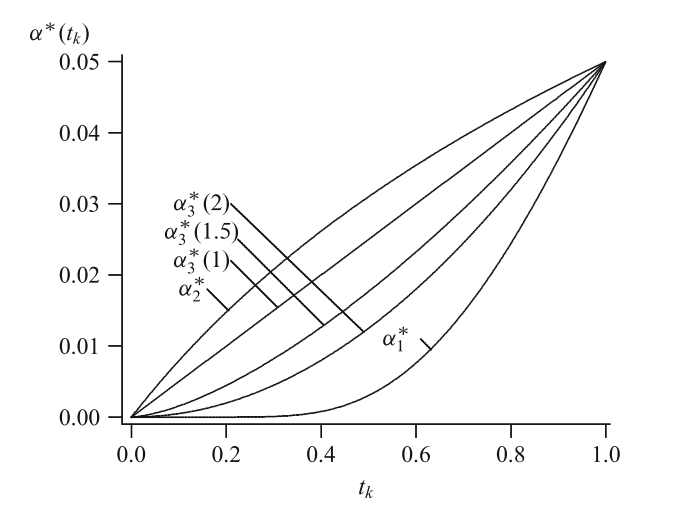
The Use Function Approach

• Computation of critical values does not depend on future information rates

• Accounting for random under- and overrunning is possible

• Specifically applicative for survival data

• Number of interim analyses need not be fixed in advance

• Planning is usually based on assuming equidistant information rates but can also be performed for suitably chosen information rates

• Do not change sample size or analysis time in a data driven way!

With rpact

library(rpact)
getDesignGroupSequential(alpha = 0.05, 
        kMax = 5, typeOfDesign = "asOF") |>
    plot(type = c(1, 4)) 

Compare designs

• Common parameter: expected and maximum sample size (“inflation factor”)

• Also: early stopping probabilities

• Assessment of futility criteria

• All can easily be done with the rpact getDesignCharacteristics() function:

designPocock <- getDesignGroupSequential(
    alpha = 0.025,
    beta = 0.2,
    kMax = 3,
    typeOfDesign = "P"
)
designOBrienFleming <- getDesignGroupSequential(
    alpha = 0.025,
    beta = 0.2,
    kMax = 3,
    typeOfDesign = "OF"
)
getDesignCharacteristics(designPocock)

Group sequential design characteristics

• Number of subjects fixed: 7.8489
• Shift: 9.1548
• Inflation factor: 1.1664
• Informations: 3.052, 6.103, 9.155
• Power: 0.2937, 0.6009, 0.8000
• Rejection probabilities under H1: 0.2937, 0.3072, 0.1991
• Futility probabilities under H1: 0, 0
• Ratio expected vs fixed sample size under H1: 0.8186
• Ratio expected vs fixed sample size under a value between H0 and H1: 1.0680
• Ratio expected vs fixed sample size under H0: 1.1547

getDesignCharacteristics(designOBrienFleming)

Group sequential design characteristics

• Number of subjects fixed: 7.8489
• Shift: 7.9855
• Inflation factor: 1.0174
• Informations: 2.662, 5.324, 7.985
• Power: 0.03292, 0.44240, 0.80000
• Rejection probabilities under H1: 0.03292, 0.40948, 0.35760
• Futility probabilities under H1: 0, 0
• Ratio expected vs fixed sample size under H1: 0.8562
• Ratio expected vs fixed sample size under a value between H0 and H1: 0.9831
• Ratio expected vs fixed sample size under H0: 1.0149

Confirmatory Adaptive Designs

Confirmatory Adaptive Designs: Basics

“Confirmatory adaptive” means:

Planning of subsequent stages can be based on information observed so far, under control of an overall Type I error rate.

Definition

A confirmatory adaptive design is a multi-stage clinical trial design that uses accumulating data to decide how to modify design aspects without compromising its validity and integrity.

Adaptive Test Procedures: The Beginning

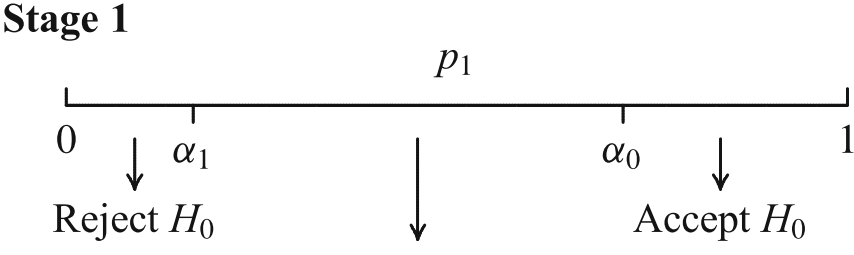
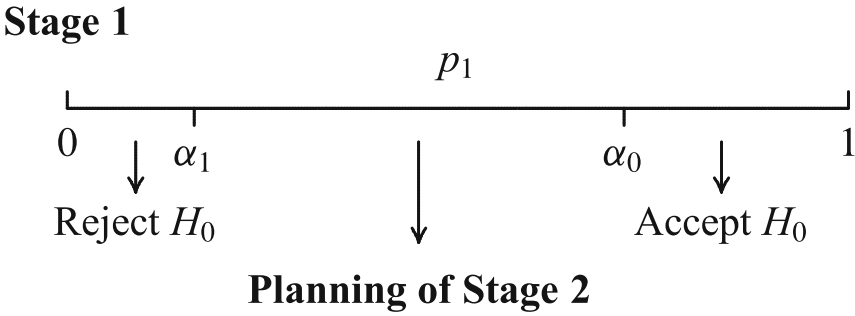
• A trial is performed in two stages

• In an interim analysis the trial may be

  • stopped for futility or efficacy or
  • continued and possibly adapted (sample size, test statistics)

• Adaptation of the design for second stage

  • adaptations depend on all (unblinded) interim data including secondary and safety endpoints
  • the adaptation rule is not (completely) preplanned

How to construct a test that controls the Type I error?

Two Pioneering Proposals

Proposals

Bauer and Köhne (1994): Combination of \(p\,\)-values with a specific combination function (Bauer 1989)

Proschan and Hunsberger (1995): Specification of a conditional error function.

The Combination Test (Bauer ’89, Bauer & Köhne ’94)

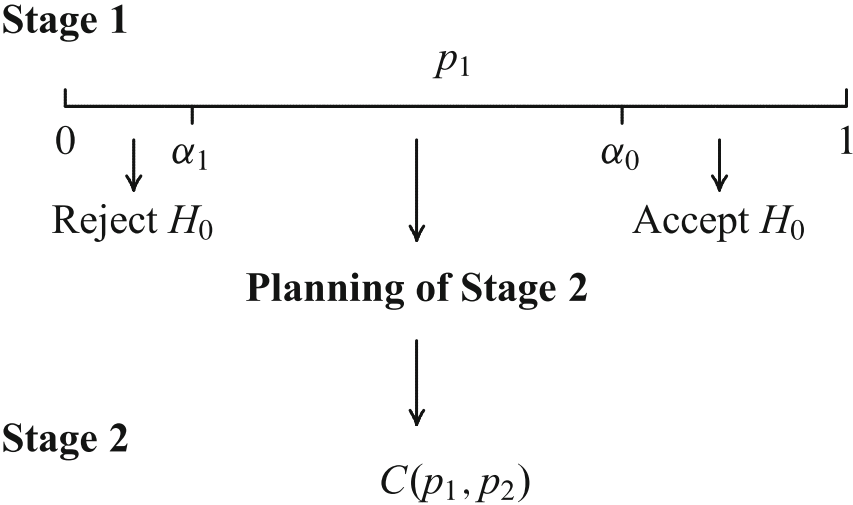
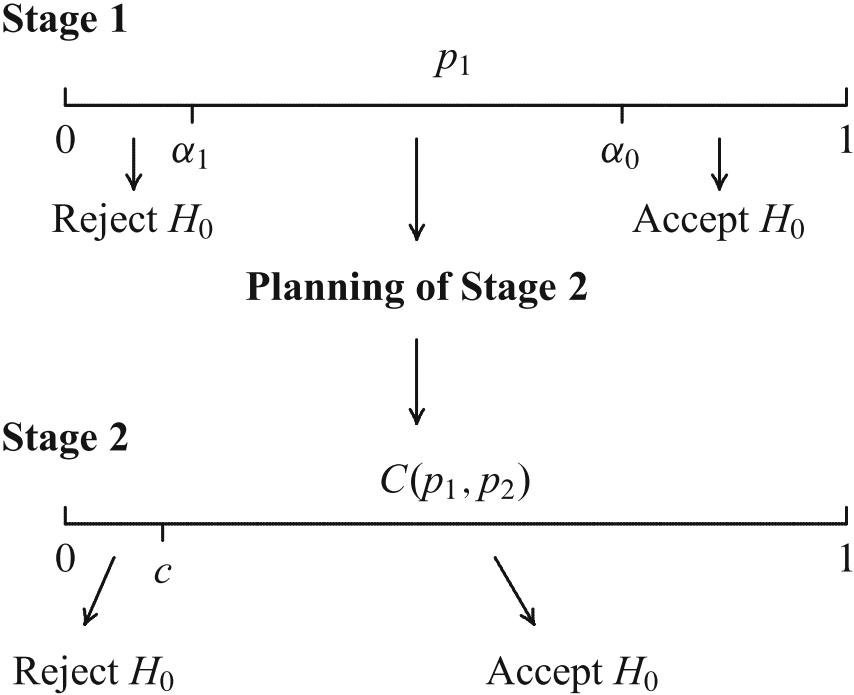
Stopping boundaries and combination function have to be laid down a priori!

Clue of the Adaptive Test

• Do not pool the data of the stages, combine the stage-wise \(p\,\)-values.

• Then the distribution of the combination function under the null does not depend on design modifications and the adaptive test is still a test at the level \(\alpha\) for the modified design.

• In the two stages, different hypotheses \(H_{01}\) and \(H_{02}\) can be considered, the considered global test is a test for \(H_0 = H_{01} \cap H_{02}\).

• Or there are multiple hypotheses at the beginning of the trials and maybe some selected.

• Or there will be even hypotheses to be added at an interim stage (not of practical concern).

Clue of the Adaptive Test

• The rules for adapting the design need not to be prespecified!

• The combination test needs to be prespecified:

  • Bauer and Köhne (1994) proposed Fisher’s combination test (\(p_1 \cdot p_2\)) but also mentioned other combination tests, e.g., the inverse normal combination test (\(w_1 \Phi^{-1}(1 - p_1) + w_2 \Phi^{-1}(1 - p_2)\) ).

  • It was shown that the inverse normal combination test has the decisive advantage that then the adaptive confirmatory design simply generalizes the group sequential design (Lehmacher and Wassmer 1999).

  • So (initial) planning of an adaptive design is essentially the same as planning of a classical group sequential design and the same software can be used.

  • An equivalent procedure (not based on p-values but based on weighted \(Z\) score statistic) was proposed by Cui, Hung, and Wang (1999) .

Possible Data-Dependent Changes of Design

• Sample size recalculation

• Change of allocation ratio

• Change of test statistic

• Flexible number of looks

• Treatment arm selection (seamless phase II/III)

• Population selection (population enrichment)

• Selection of endpoints

For the latter three, in general, multiple hypotheses testing applies and a closed testing procedure can be used in order to control the experimentwise error rate in a strong sense.

Seamless Phase II/III Trials: Treatment Arm Selection

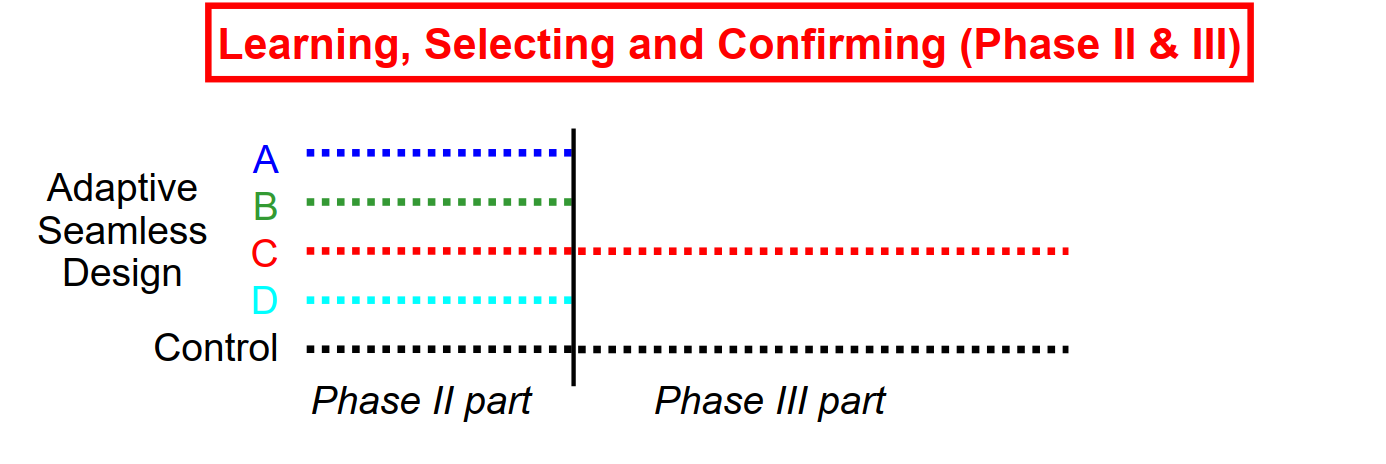
• Conduct phase II trial as internal part of a combined trial

• Plan phase III trial based on data from phase II part

• Conduct phase III trial as internal part of the same trial

• Demonstrate efficacy with data from phase II + III part

Enrichment: Phase 2/3 Study in HER2- Early Stage BC

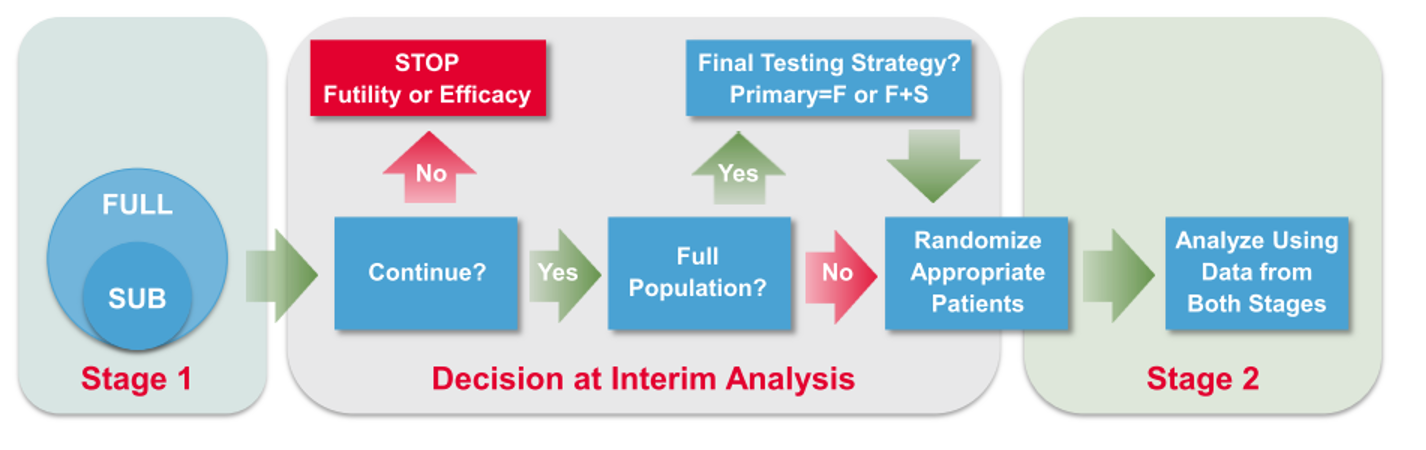
• Stage 1 objective

  • Stop for futility/efficacy

  • To continue with HER2- (Full) population – Broad Label (F) or Enhanced Label (F+S)

  • To confirm greater benefit in TNBC Subpopulation – Restricted Label (S)

  • To adjust the sample size

• Stage 2 data and the relevant groups from Stage 1 data combined

Sources for alpha Inflation

• Interim analysis

• Sample size reassessment

• Multiple hypotheses

Adaptive Designs with Treatment Arm Selection

Multi-Stage Closed Adaptive Tests

• Originally proposed in Bauer and Kieser (1999); Lehmacher, Kieser, and Hothorn (2000); Hommel (2001); …

• Combines two methodology concepts: Combination Tests and Closed Testing Principle

• Fulfills the regulatory requirements for the analysis of adaptive trials as it strongly controls the prespecified familywise error rate

• Does not require a predefined selection and/or sample size recalculation rule

• Methods for predefined selection rules (Stallard and Todd (2003); Magirr, Stallard, and Jaki (2014); …) exist as well.

Strong Familywise Type I Error Rate Control

Multiple Type I error rate

Probability to reject at least one true null hypothesis.

(Probability to declare at least one ineffective treatment as effective).

\(\hspace{1.6cm}\)

Strong control of multiple Type I error rate

Regardless of the number of true null hypotheses (ineffective treatments): \[\text{Multiple Type I error rate }\le \alpha\]

Two-Stage Closed Testing Principle, 3 Hypotheses, select one

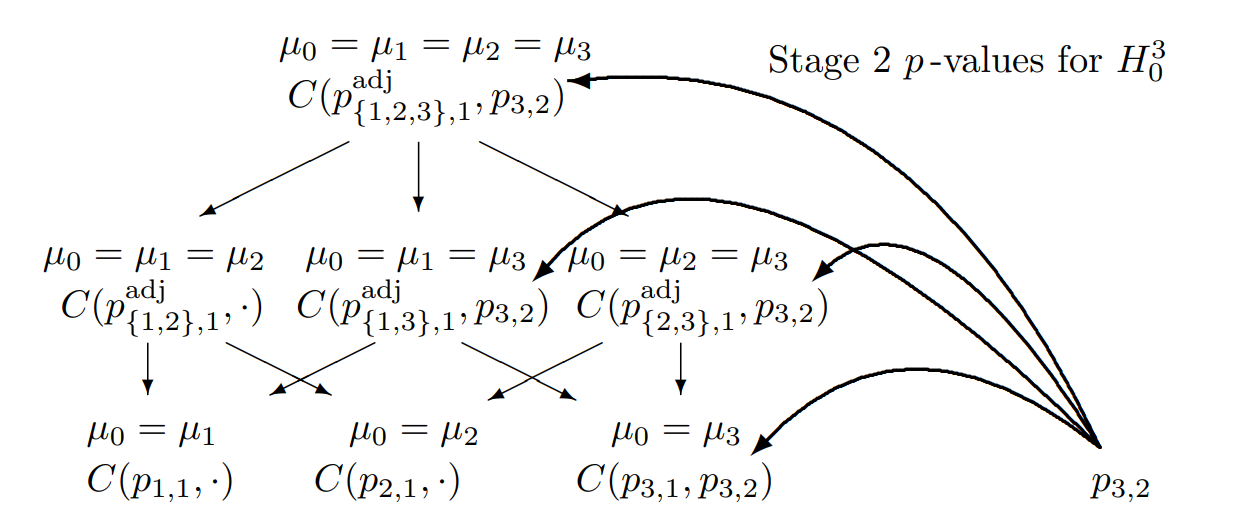
Combination tests to be performed for the closed system of hypotheses (\(G = 3\)) for testing hypothesis \(H_0^3\) if treatment arm 3 is selected for the second stage

Two-Stage Closed Testing Principle, 3 Hypotheses, select two

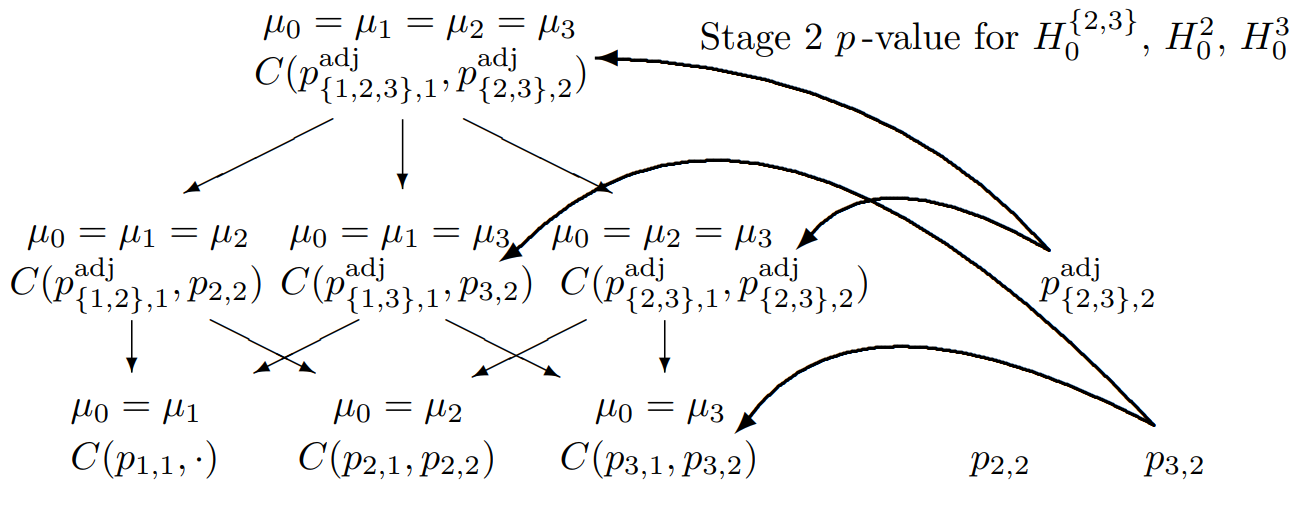
Combination tests to be performed for the closed system of hypotheses (\(G = 3\)) for testing hypothesis \(H_0^3\) if treatment arms 2 and 3 are selected for the second stage

Adaptive Designs with Treatment Arm Selection

• Available in rpact

• Can be applied to selection of one or more than one treatment arm. The number of selected arms and the way of how to select treatment arms needs not to be preplanned.

• Choice of combination test is free.

• Data-driven recalculation of sample size is possible.

• Choice of intersection tests is free. You can choose between Dunnett, Bonferroni, Simes, Sidak, hierarchical testing, etc.

• For two-stage designs, the CRP principle can be applied: adaptive Dunnett test (König et al. (2008), Wassmer and Brannath (2016), Section 11.1.5).

• Confidence intervals based on stepwise testing are difficult to construct. This is a specific feature of multiple testing procedures and not of adaptive testing. Posch et al. (2005) proposed to construct repeated confidence intervals based on the single step adjusted overall p-values.

Discussion

The Critism from the Statistical Perspective

• Non-correctness of the procedure
• Reluctance to accept connection between adaptive and group sequential designs
• Inefficiency as compared to classical group sequential or other designs, violating the sufficiency principle
• Uncertainty of interim information
• Construction of confidence intervals and bias adjusted estimates not possible.

None of these critisms are sustainable

The Regulatory Perspective

• Adaptive designs per se seem to be accepted by the agencies for regulatory research as long as a detailed plan is provided, e.g., requirement for prospectively written standard operating procedures.
• Do not use too many interim analysis.
• Do not perform too early interim for showing efficacy.
• Guidance advise against operational bias, e.g., treatment effect may be deduced from knowledge of adaptive decision. Sponsor has to take care of that!
• Support study design through comprehensive simulation reports.

Careful application but principal acceptance

Final Remarks

• Adaptive designs are more complicated than fixed or group-sequential designs in terms of trial planning, logistics, and regulatory requirements to ensure trial integrity and avoid operational bias.

• In most cases, simulations are necessary in order to assess properties of adaptive strategies and decide whether an adaptive design is appropriate.

• In the meantime, there is some clarification of how and when to use an adaptive design.

• Some concern being caused by unblinding the study results. This is an inherited problem!

• Commonly accepted that a group sequential design can be made more flexible through the use of the inverse normal combination test.

• Increasing use of Bayesian methodology.

Final Remarks

• Software available (ADDPLAN, EaSt, nQuery, gsDesign, rpact, SAS, etc.)

• Most important applications

  • Sample size recalculation
  • Treatment arm selection designs
  • Population enrichment designs

• Many applications run so far, overview papers / books exist.

• Report in journals often do not mention the use of adaptive designs.

• There are successful examples of carefully planning and performing adaptive confirmatory designs.

References

Bauer, P. 1989. “Multistage Testing with Adaptive Designs.” Biometrie Und Informatik in Medizin Und Biologie 20: 130–48.

Bauer, P., and M. Kieser. 1999. “Combining Different Phases in the Development of Medical Treatments Within a Single Trial.” Statistics in Medicine 34: 1833–48.

Bauer, P., and K. Köhne. 1994. “Evaluation of Experiments with Adaptive Interim Analyses.” Biometrics, 1029–41.

Cui, L., H. M. J. Hung, and S.–J. Wang. 1999. “Modification of Sample Size in Group Sequential Clinical Trials.” Biometrics 55: 853–57.

Friede, Tim, and Meinhard Kieser. 2001. “A Comparison of Methods for Adaptive Sample Size Adjustment.” Statistics in Medicine 20 (24): 3861–73.

———. 2006. “Sample Size Recalculation in Internal Pilot Study Designs: A Review.” Biometrical Journal 48 (4): 537–55.

Gould, A. L. 1992. “Interim Analysis for Monitoring Clinical Trials That Do Not Materially Affect the Type I Error Rate.” Statistics in Medicine 11: 53–66.

Hommel, G. 2001. “Adaptive Modifications of Hypotheses After an Interim Analysis.” Biometrical Journal 43: 581–89.

Kieser, M., and T. Friede. 2000. “Re–Calculating the Sample Size in Internal Pilot Study Designs with Control of the Type I Error Rate.” Statistics in Medicine 19: 901–11.

König, F., W. Brannath, F. Bretz, and M. Posch. 2008. “Adaptive Dunnett Tests for Treatment Selection.” Statistics in Medicine 27: 1612–25.

Lehmacher, W., M. Kieser, and L. Hothorn. 2000. “Sequential and Multiple Testing for Dose–Response Analysis.” Drug Information Journal 34: 591–97.

Lehmacher, W., and G. Wassmer. 1999. “Adaptive Sample Size Calculations in Group Sequential Trials.” Biometrics 55 (4): 1286–90.

Magirr, D., N. Stallard, and T. Jaki. 2014. “Flexible Sequential Designs for Multi-Arm Clinical Trials.” Statistics in Medicine 33: 3269–79.

Posch, M., F. König, M. Branson, W. Brannath, C. Dunger–Baldauf, and P. Bauer. 2005. “Testing and Estimating in Flexible Group Sequential Designs with Adaptive Treatment Selection.” Statistics in Medicine 24: 3697–3714.

Proschan, M. A., D. A. Follmann, and M. A. Waclawiw. 1992. “Effects on Assumption Violations on Type I Error Rate in Group Sequential Monitoring.” Biometrics 48: 1131–43.

Proschan, M. A., and Sally A. Hunsberger. 1995. “Designed Extension of Studies Based on Conditional Power.” Biometrics, 1315–24.

Stallard, N., and S. Todd. 2003. “Sequential Designs for Phase III Clinical Trials Incorporating Treatment Selection.” Statistics in Medicine 22 (5): 689–703.

Wassmer, Gernot, and Werner Brannath. 2016. Group Sequential and Confirmatory Adaptive Designs in Clinical Trials. Springer. https://link.springer.com/book/10.1007/978-3-319-32562-0.

Wittes, J., and E. Brittain. 1990. “The Role of Internal Pilot Studies in Increasing the Efficiency of Clinical Trials.” Statistics in Medicine 9: 65–72.